Задания 1-5 ОГЭ 2021
(На странице использованы задания из открытого банка заданий fipi.ru)
Задание 1 . Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.

Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
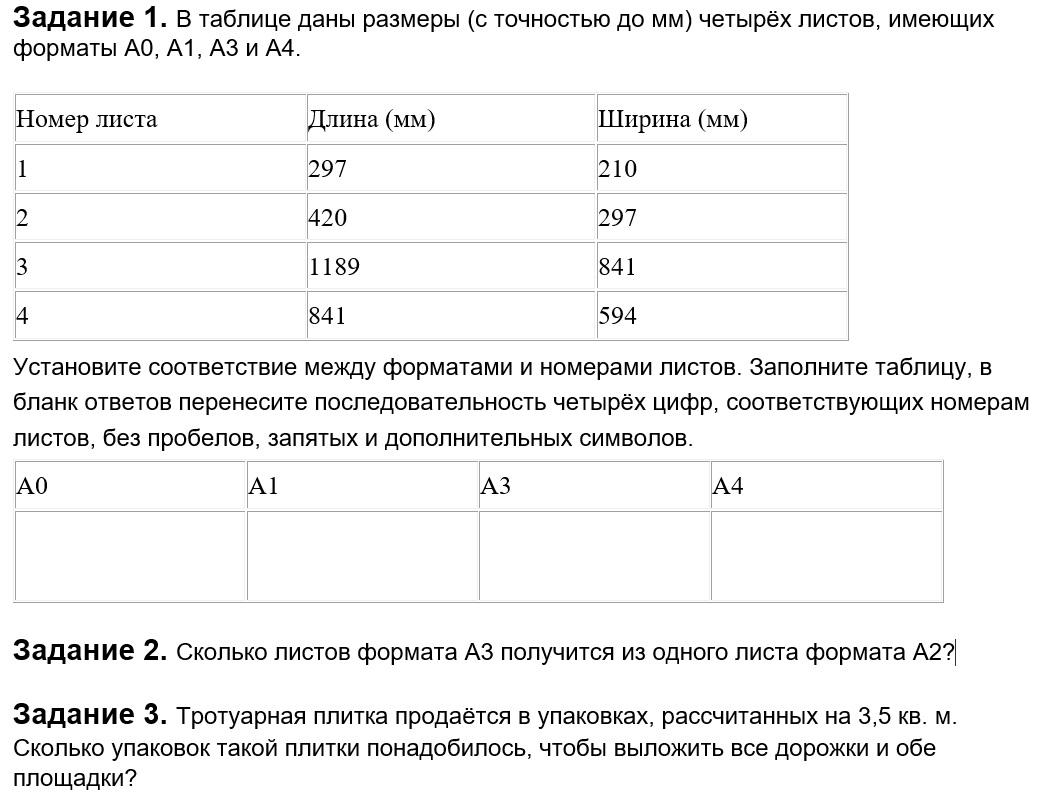
1. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А1, А2, А3 и А5
Установите соответствие между форматами и номерами листов. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
|
2. Сколько листов формата А3 получится из одного листа формата А2?
3. Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
4.Найдите длину листа бумаги формата А7. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 5.
5. Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
Задание 2. Прочитайте внимательно текст и выполните задания 15.

На плане изображено домохозяйство по адресу: СНТ «Прибор»,
2-я Линия, д. 26 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится гараж, а слева в углу участка расположен сарай, отмеченный на плане цифрой 1. Площадь, занятая сараем, равна 24 кв. м.
Жилой дом находится в глубине территории и обозначен на плане цифрой 6. Помимо гаража, жилого дома и сарая, на участке имеется летняя беседка, расположенная напротив входа в дом, и мангал рядом с ней. На участке также растут ели. В центре участка расположен цветник.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером . Перед гаражом и между домом и беседкой имеются площадки площадью 40 и 16 кв. м соответственно, вымощенные такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
|
2.Найдите площадь, которую занимает цветник. Ответ дайте в квадратных метрах.
3. Тротуарная плитка продаётся в упаковках, рассчитанных на 3,5 кв. м. Сколько упаковок такой плитки понадобилось, чтобы выложить все дорожки и обе площадки?
4. Сколько процентов площади всего участка занимает сарай?
5. Хозяин участка планирует установить в жилом доме систему отопления.
Он рассматривает два варианта: электрическое или газовое отопление. Цены
на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
|
|
Нагреватель (котёл) |
Прочее оборудование |
Средн. расход газа/ средн. потребл. мощность |
Стоимость газа/электро-энергии |
|
Газовое отопление |
28 000 руб. |
16 540 руб. |
1,1 куб. м/ч |
4,8 руб./куб. м |
|
Электр. отопление |
22 000 руб. |
14 444 руб. |
5,8 кВт |
4,4 руб./(кВт*ч) |
Обдумав оба варианта, хозяин решил установить газовое отопление. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости покупки
и установки газового и электрического оборудования?
Задание 3

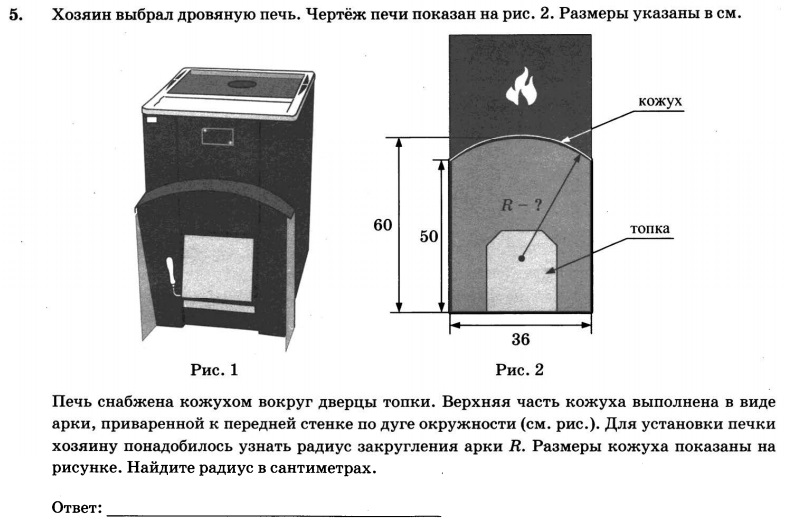
Задание 4


Задание 5
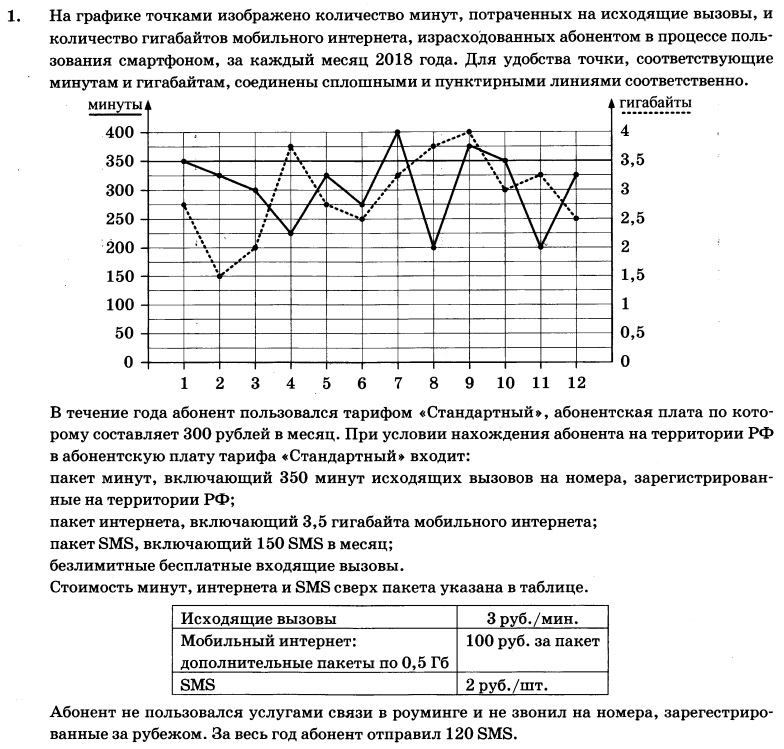

Задание 6

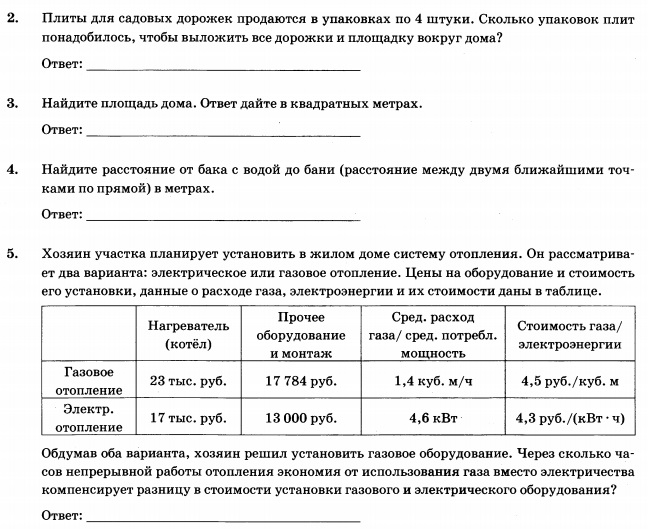
Задание 7